The Blackbird is the Composition of Composition and Composition

Combinatory logic is a very strange branch of computer science. It's too much on the math side to be well-known among programmers, and yet it's so stupidly simple that it would take any programmer around 5 minutes to implement the complete set of common combinators in a modern programming language of their choice, regardless of how much they know or care about the topic. Needless to say, a weird niche has formed around it.

Despite their simplicity, combinators have a way of frying your brain. The title of this post is an example of a sentence that fried mine, so this is an attempt at processing it in a way that makes sense to me (and hopefully readers who are not familiar with this topic yet!). Oh, and in case you're wondering about the "blackbird" in the title: giving combinators bird names is a thing for some reason.¹

What's a combinator, exactly?

Conceptually, combinators are generic higher-order functions (functions that can have other functions as inputs and outputs) that can only use function application in their implementation. They cannot use any functions other than the ones provided (or other combinators) and they can only apply those functions. No conditionals, no use of specific values. An interesting property of combinators is that their signature already tells you what they do, because every combinator's signature is unique².

Confused yet? Take this example of a type signature:

a -> b -> a

This describes a function that takes an a and returns yet another function that takes a b and returns an a. This is the same as a -> (b -> a) (but not (a -> b) -> a³). a and b are type variables and could be substituted by any concrete type. There is only one way to write a self-contained function with this signature. It's this:

const :: a -> b -> a -- type signature
const x = \y -> x -- definition (x is a parameter, \y -> x is a lambda)

For any value x, the const function gives you a function that always returns x. Now, this combinator actually doesn't even use function application - the one thing that is allowed in combinators – there's simply no function to apply. It still meets the criteria for a combinator though. Here's an even simpler one, the identity function:

id :: a -> a
id = \x -> x

Again, there is only one combinator that can possibly have the signature a -> a, and it's this one.

Combinators in Array Programming

My first conscious introduction to combinatory logic was when I learned BQN around two years ago due to how prevalent it is in its style of code. This comes from the APL tradition, a family of languages that, much like combinatory logic, has a similarly weird (and probably mostly overlapping) niche in computer science. I find combinators in APL-style languages fairly easy to get the hang of, and I think there are mainly two reasons for this:

• Functions can only have 1 or 2 arguments, and combinators handle both cases sensibly
• Combinators are (usually) not implemented as functions, but as a separate function-like construct ("modifiers" in BQN's case)

The latter means that combinatory logic stays on one level of abstraction; you can combine functions, but not combinators themselves.

Today, I want to focus on a single combinator called composition ("atop" in BQN lingo). Here it is, depicted as a diagram taken from the BQN documentation. It shows the two cases: either you call F∘G with one or with two arguments. If you call it with one, it gets passed to G, then F; if you call it with two, both get passed to G and the result from that gets passed to F.

The thing you might be asking yourself right now is: "Why? Why would I ever use atop if I can just... call one function, and then another?"

The main answer (and this goes for combinatory logic in any language) is enabling point-free aka tacit programming. This is a style of programming where you define functions in terms of the space they operate on rather than individual points in that space. This can make code quite concise and, I would argue, in some cases easier to understand. Not always, and not if you're unfamiliar with the "shape" of the combinators that are used – but once you get a feel for a certain combinator, it's easy to recognise its pattern and quickly find the meaning of code that uses it. Here's a classic example from APL, the average function:

+⌿ ÷ ≢

These are just three functions: Sum (plus reduce), divide and length (tally). In other words, "sum divided by length", which is the definition of the average of a list of numbers. This is called a train in APL-style languages but is also known as the Phi (Φ) combinator. Its result applies the two outer functions to the argument and then combines them with the function in the middle. Notice how there is no mention of any parameter (point) here – point-free programming. Once you internalise this pattern of just writing three functions next to each other, it's not hard to understand anymore. Just for comparison, here's the same function with the input as an explicit parameter (ω)⁴:

{(+⌿ ω) ÷ (≢ ω)}

Combinators in Haskell

As I said before, it's not possible to combine combinators using combinators in APL, BQN and similar, i.e., there are no meta-combinations. This is, in some sense, a limitation. It makes perfect sense to write combinators as functions after all, as seen earlier. Here's composition (atop) as a Haskell function:

comp :: (b -> c) -> (a -> b) -> a -> c
comp f g = \x -> f (g x)

Read: the composition of functions f and g is a function that takes an argument x and returns f (g x) (f applied to g applied to x). Function application (commonly denoted f(x) in other languages) in Haskell is just written by putting the argument next to the function (f x).

If the type signature confuses you: It just says that:

• f is a function that takes a b and returns a c
• g is a function that takes an a and returns a b
• the result is a function that takes an a and returns a c

Again, this works for anything a, b and c may be (type variables).

 -------   comp f g    ------- 
(   a   )------------>(   c   )
 -------               ------- 
       \               /       
      g \             / f      
         \           /         
          \ ------- /          
           (   b   )           
            -------            

There is one more important thing I left out that you need to understand before we can try to reason about what it means to combine combinators. One of the fundamental ideas in Haskell is that functions really only have one parameter. If you want to have multiple parameters, you define a function that returns another function. In fact, when you write something like

f a b = a + b

(where a and b are parameters of function f), this happens automatically. The type signature of f is

f :: Int -> Int -> Int

(a function taking an Int, returning another function taking an Int, returning an Int). So, when you type f 3 5 to calculate 3 + 5, what actually happens is this:

1. First, f 3 is computed, the result of which is a new function (let's call it f') with the signature f' :: Int -> Int and which is defined as f' b = 3 + b
2. Then, f' 5 is computed, returning 3 + 5

Thus, f 3 5 is the same as (f 3) 5. And you could also "just" write f 3, which will give you a function adding 3 to any input.

This has some useful and (mostly mathematically) interesting properties, such as uniformity (if something can work with a generic function of one parameter, it can work with a function of any amount of parameters). It also means that the previously defined combinators can be rewritten without lambdas:

const x y = x
id x = x
comp f g x = f (g x)

With this in mind, something like comp f suddenly makes sense: this gives you a function "waiting" for another function g which then returns the composition of f and g. The reason I split the earlier definitions into "outer" and "inner" parameters using lambda expressions was to make it clearer to non-Haskellers what the combinators actually do. Technically speaking however, there is no difference between those.

Combining combinators

So, we've seen the composition combinator that acts like a kind of pipe: apply g, then f. This combinator is actually built in to Haskell as an (infix) function named . (where do I put my full stop now?). In contrast to how composition works in APL-style languages, . will only produce functions that "pipe" a single parameter. But let's say we have one function that takes two parameters, and another function that takes one parameter and that we want to pipe from the binary to the unary function like so:

bicomp f g = \x y -> f (g x y)

This is basically the same as composition, except that g gets two arguments instead of just one. And this is what's known as the infamous "blackbird" combinator. Well, congratulations to me I guess, because this definition is valid and does exactly what we want. However, the twisted minds of lambda calculus magicians have come up with this wicked definition (it really is the same thing):

(.) . (.)

WTF.

I first saw this in a (really good) Strange Loop 2016 talk by Amar Shah. It's the same as (.) (.) (.) (prefix notation) or comp comp comp (using our own definition from earlier). But even days after thinking about it and asking a friend who is good with Haskell, I was still left like this:

Now, I know that you can prove that this makes sense using the type signatures, which has you do a bunch of substitutions until you get from (.) :: (b -> c) -> (a -> b) -> a -> c to (.) . (.) :: (b -> c) -> (a1 -> a2 > b) -> a1 -> a2 -> c (basically doing the compiler's work by hand). But this doesn't answer my question: what in the world does it mean to compose composition with composition? How do you get an intuition for this?

I found that I was lacking a visual aid. What I like about BQN's documentation (excerpts above) is that it gives you a sort of flow chart for all its combinators. I thought maybe I could come up with something like that to help me get how the hell (.) . (.) works.

A combinator flow chart

Combinators are simple, but a visual representation must still support multiple elements:

• input parameters
• function application
• partial provision of parameters (e.g. something like comp f must be representable, even though the second function is missing)

Here's the syntax I came up with:

You can read these graphs from top to bottom. Inputs are at the top (note that their order is from left to right), outputs come out of function application. Partial application is also representable: just substitute one of the inputs and leave the others. The graph above represents the combinator that just applies a function to an argument, defined like this:

apply :: (a -> b) -> a -> b
apply f x = f x

Here's another one, the flip combinator:

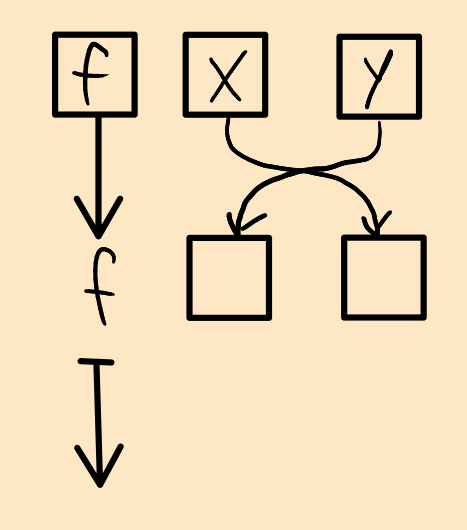
flip :: (a -> b -> c) -> b -> a -> c
flip f x y = f y x

Finally, here's the one for comp/(.):

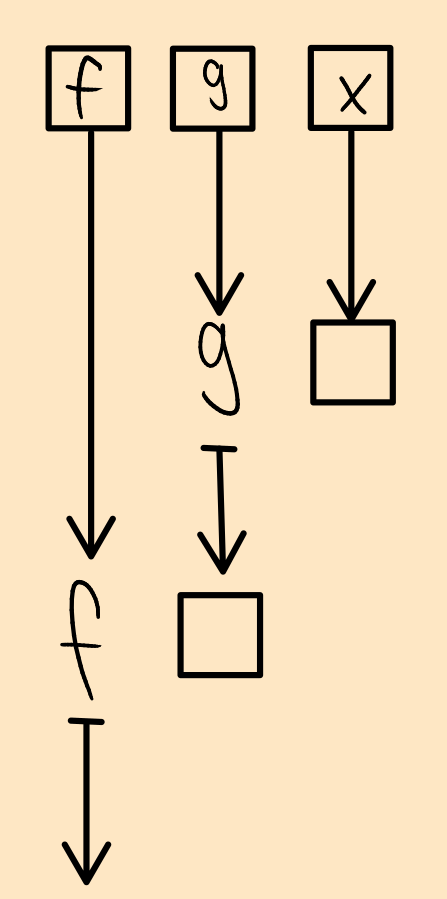
Now, let's see what happens when we input comp and comp as f and g.

Composing composition and composition

To do this, we partially apply comp to itself, thus getting rid of the f and g inputs and substituting their appearances in the original graph with the original graph itself. Structurally, we'll get something like this:

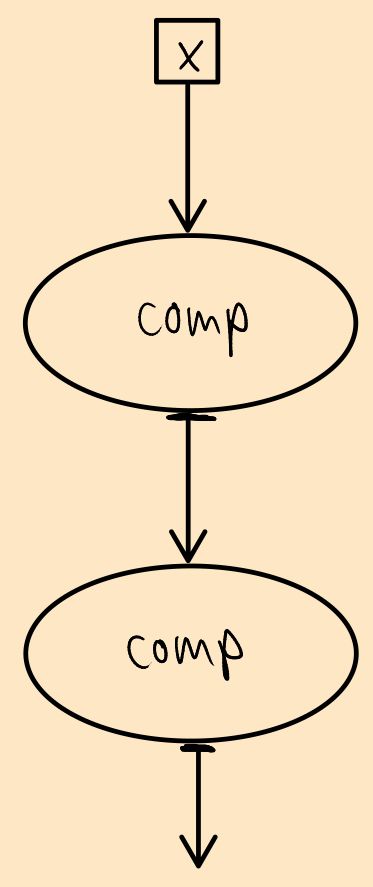
What we get back looks at first glance like it's a function that only takes a single parameter, but we know that we must get a function that takes 4:

1. f (b -> c)
2. g (a₁ -> a₂ -> b)
3. x (a₁)
4. y (a₂).

And don't worry, we'll get there. The first parameter (called x in the above sketch) is actually a function f, so let's call it that. And then let's actually expand the sketch above to its full representation. I present to you, the composition of composition and composition:

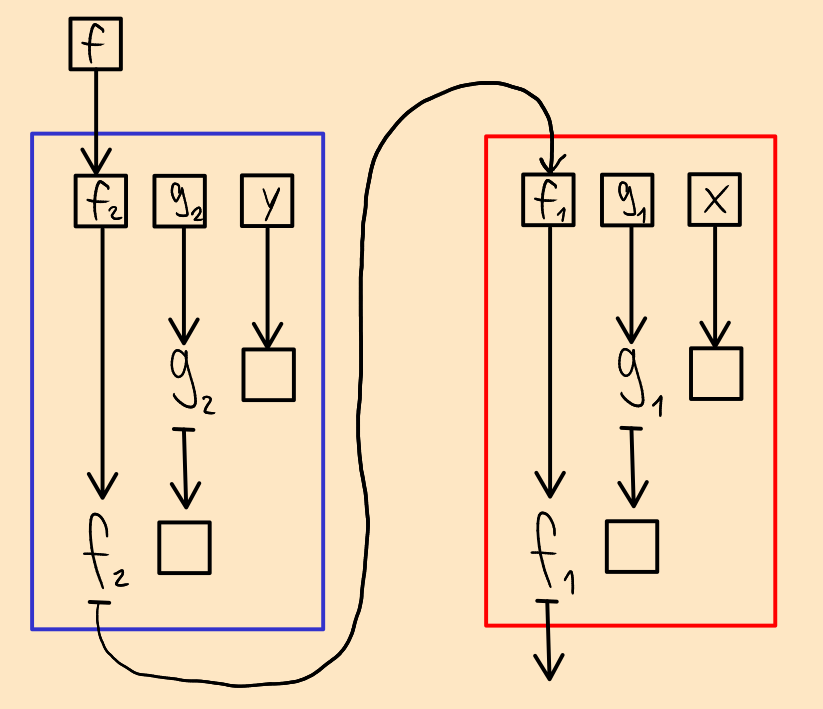
For obvious reasons of space efficiency, I've decided to put the second comp on the right side rather than below the first one. I also put colourful retangles around the two individual comps; they have no meaning for this graph, but they might still be helpful to understand the following simplifications.

What we see here is that the left half is used as input (f1) for the right half. So let's put it there directly:

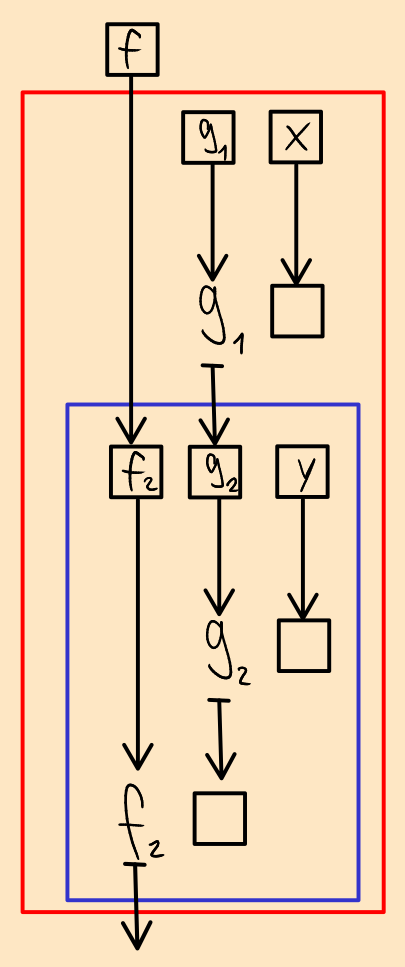
As you can see, the function that we give as input to the whole thing just ends up in the composition that used to be on the left. In other words: f2 = f. Let's remove that redundancy:

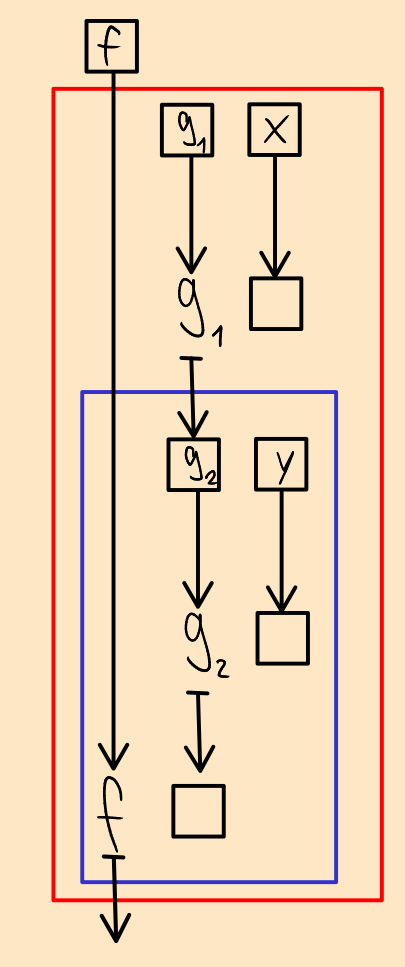
A similar thing now becomes apparent for the gs: g2 is the result of of applying g1 to x. This means that applying g2 to y is the same as applying g1 to x and the result of that to y. In other words: g2 y = g1 x y. Let's skip the middleman then and just give the two arguments to g1 directly. And while we're at it, since there is now only a single g left, let's just call it g.

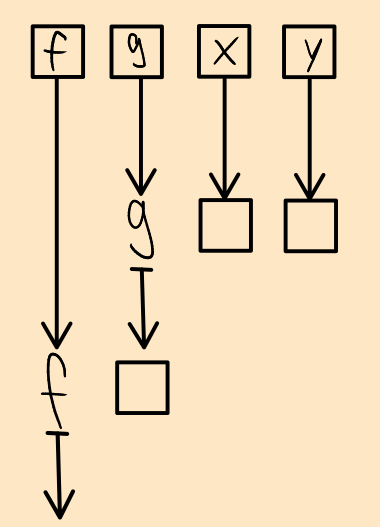
And there we have it – the blackbird!

Untying the knot in my brain

I think I at least partially succeeded at my mission to make meta-combinations more comprehensible. (.) . (.) did not make sense to me at all – now I sort of understand what's going on, even though I still don't find it intuitive. I'm curious to see for how many other combinators my visualisation is useful. For example, I have an itch to try to graph the infamous Y combinator and make sense of it that way. Maybe in a future post... Until then, feel free to tell me if you're part of the birdwatchers now or if I lost you at some point in this post.