Immutable Collections are Fast (Enough)

1. Naive Immutability
2. Persistence
3. Raw Performance
4. Conclusion

A couple of months ago, a few people, including myself, discussed how to implement breadth-first search in concrete code. As is often the case, there are multiple approaches: an imperative implementation (as shown on the Wikipedia page) and a recursive, more declarative implementation. The latter looks something like this (pseudo code, mostly taken from German Wikipedia but with an ML-style syntax):

bfs start_node goal_node = bfs' {start_node} ∅ goal_node 

bfs' fringe visited goal_node 
    | fringe == ∅ = False
    | goal_node ∈ fringe = True
    | otherwise = bfs' ({child | x ∈ fringe, child ∈ children x} ∖ visited) (visited ∪ fringe) goal_node

There are a couple of interesting things to note about this implementation. First, just in case you're a bit lost:

• The purpose of this specific variant is to check whether a node is contained in a tree. You could also easily modify it to find a path to a specific node or perform an action for each encountered node.
• This pseudo code uses mathematical set notation:
  • x ∈ S means x in S or S.contains(x)
  • ∅ means "empty set"
  • S ∪ T means "union of S and T" or S + T
  • S ∖ T means "difference of S and T" or "S without T"
  • {child | x ∈ fringe, child ∈ children x} is a set comprehension - the set that you get when you put all children of all fringe nodes in one set in this case.

This solution is very elegant and certainly concise, but some readers may have noticed the main requirement for it to work: The sets need to be immutable.

In particular, this means that ∪ and ∖ need to produce new sets instead of modifying their inputs. In mathematics, this seems obvious; sets are values and you can't just "change" them, just like you can't "change" the number 41 by writing 41 + 1. In programming however, things are not this simple anymore. Our programs only perform practical and concrete, not abstract mathematical computation, right?

...Well, of course not. If the above statement were true, we would all still be stuck writing assembly. What is true about this though is the fact that every "abstract mathematical computation" we use in our code needs to be implemented in concrete terms somewhere down the line.

So, this raises an obvious question: how expensive (in terms of performance) is it to use a more mathematical approach to collections in our program? And are the benefits (such as more "elegant") implementations worth it?
I'm not here today to answer the second, almost philosophical question; rather, I would like to take a look at whether it is even possible to use immutable collections at scale and if so, at least give an idea of the how.

Naive Immutability

There is a very simple way to implement an immutable collection, for example an immutable list: simply don't define an add or remove method. In fact, that sums up what Java's own immutable lists do. It's stupidly easy to do: Just encapsulate an Array and define a get and perhaps an iterator method and you're done. Unfortunately, this doesn't work too well in Java's case because the Collection interface requires you to implement methods for mutation, but that's a whole different story.

In any case, this approach has an significant flaw for general use: we do want to add and remove elements, it's just that we want a new collection for each of those operations.
Again, there is a very naive implementation - all we need is a function to copy immutable collections to mutable ones and vice versa.

def immutable_add(immutable_coll, element):
    temp = mutable_copy(immutable_coll)
    add(temp, element)
    return immutable_copy(temp)

Great, now we can "modify" immutable collections too, so we have everything we need to use them in real applications. Except... copying the entire list for every modification may not always be the best idea.

Persistence

Copying takes linear time and space - this is not good for an operation as fundamental as adding or removing elements. It may not be a problem as long as we're working with rather small collections, but as our collections grow, so do the time and memory it takes to add and remove elements. This is not true for most mutable collections: inserting an element into a java.util.HashSet always takes the same amount of time - no matter how big the set is. Actually, that is not entirely correct: it takes the same amount of time from an amortised perspective, which means that there may be spikes in singular individual operations (because the internal array needs to be resized at certain points), but this is not relevant to the point. The point is: it is much better than linear complexity.

So, how do we solve this problem and make immutable collections actually viable? The answer is persistent collections.

In essence, persistent collections vastly improve the performance of naive immutability. They do so by sharing (some of) the unchanged structure of the old version with the new version of a collection instead of copying everything for every modification. This, in itself, leverages the properties of immutability: Because the collection is immutable, one can use the same bits of data in two different collections. To show an example of what "sharing structure" means, here is a Kotlin implementation of the simplest persistent data structure there is: the persistent singly-linked list (aka. just "list" in ML-like languages and many Lisps):

data class PersistentList<E>(val head: E, val tail: PersistentList<E>?) {

    fun push(element: E) = PersistentList(element, this)
    
}

This is just one way to implement it; one notable property of this implementation is that null is considered the empty list.

What we now have, essentially, is an immutable LIFO stack. We "add" elements to the front (push), lookup the current top element (head) and pop the first element (tail) to get the list "after" it. There are a few reasons why this data structure is great:

• It is the simplest list you can possibly define - a list is just an element and possibly the rest
• It is 100% persistent, meaning the entire structure is preserved. Nothing needs to be copied for it to be immutable and insertion, lookup and deletion are all done in O(1), i.e. constant time.

The biggest disadvantage of this structure is that it is very limited. Any additional non-trivial operation on top of the existing three will not be as efficient. For example, adding to the back of the list or looking up a specific index of the list can only be done in linear time.

Fortunately, there are many other persistent collections (including ones for random access, sets and maps), although none of them are as simple as the list. One common way to implement persistent random access collections (e.g. as an alternative to the mutable java.util.ArrayList) is to use a tree structure instead of an array. You make this structure immutable, so when creating a new collection based on the old one, you can re-use nodes of that tree whose derivatives do not change in the modification.
This is an over-simplification of how this works - entire research papers have been written about efficient persistent collections and frankly, I am not enough of an expert to lay out specific implementation details here for you today.

Raw Performance

What I can do though is benchmark the raw performance of persistent collections (and java.util collections as a comparison) to get an impression of fast they actually are.
And that's exactly what I did.

TL;DR:
The benchmarks measured the following:

• How long it takes to add 1 million randomly generated strings to a collection
• How long it takes to remove 1 million randomly generated strings from a collection
• How long it takes to look up an element in a collection

The parameters for those operations vary from collection type to collection type. For stacks, "lookup" means just looking up the front element, for random access lists it means looking up a random index.

The benchmark includes many different collections from four different JVM libraries (Java, PCollections, Clojure, Kotlin). Below you can see the example results for a selection of them: Lists (random access), Stack (LIFO), Set (unordered/hash), Map (unordered/hash). Those results were generated on a machine with an i7-7700k and 32GB of DDR4-3200 RAM.

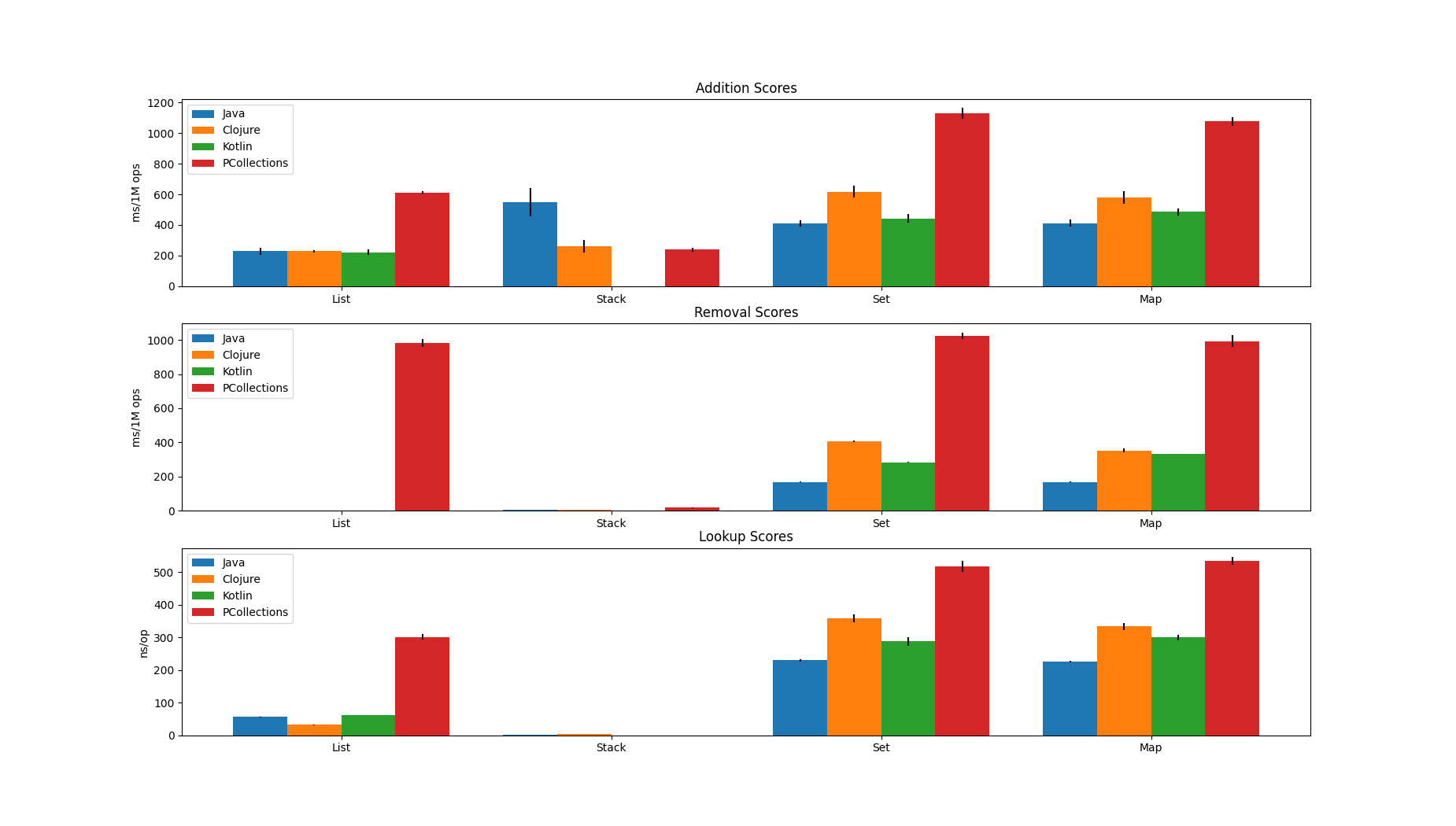
Lower scores are better, as they indicate execution time.

There are a couple of additional things to note about this data:

• Kotlin does not provide a persistent stack implementation or similar, thus there is no data in those areas.
• For the "List removal" benchmark, only PCollections results are available, because:
  • Clojure does not have indexed-based removal on its vectors
  • Java is too big of an outlier, taking around 20 seconds to remove 1M elements
  • Kotlin is an even bigger outlier, in this case taking over 200 seconds. In the other results, it did not even terminate without timing out.
• The black lines on top of the bars show the 99.9% error relative to the measurement result
• While it is hard to make out, there are indeed removal and lookup results for Stacks. They just happen to be very efficient in those cases, to an extent where the difference between the tested libraries almost becomes insignificant.

I think it is fair to say that, at least within the scope of this benchmark, persistent collections performed very well, perhaps even surprisingly well. Especially random access persistent lists/vectors can easily keep up with the mutable ArrayList. While there are bigger differences for sets and maps, those differences are probably still not big enough to be relevant in a lot of the programs you write. And there are even further optimisations for persistent collections: in Clojure and Kotlin, there are additional "transients" which are designated mutable collections used to build persistent ones quickly, while still preserving the integrity of the immutable result.

Conclusion

The performance cost of using immutable collections cannot be denied but, as you can see, it would be silly to dismiss them as too slow. I hope this short post has given you some idea of how immutability can actually be a viable alternative to the predominantly mutable code out there. That is, if you hadn't figured that out already anyway :).